Chart of the Day: Education and Spending

Since the topic in one of the comment threads has turned to education, I thought I'd put this chart up.  I may have used it before, but I can't remember.



Yes, yes, yes, I know, careful dissection of the data behind this chart coupled with alternate assumptions and premises could lead one to conclude this chart is an exaggeration, but education spending and actual educational outcomes have been at least somewhat decoupled for a half-century.

That delta $100,000+ in spending also should give us pause. Many of the recipients would likely, in my opinion, be better off with that money invested for them rather than spent trying to educate them.

The Smug

A recent Jonah Goldberg column contained the following:

I don’t know who first said, “Behind every apparent double standard lies an unconfessed single standard” (and as far as I can tell, neither does the Internet), but whoever did was onto something.

What looks like inexplicably staggering hypocrisy from the conservative perspective is actually remarkably consistent from the liberal perspective.

Well, “perspective” is probably the wrong word because it implies a conscious, deliberate, philosophical point of view. What is really at work is better understood as bias, even bigotry.

If you work from the dogmatic assumption that liberalism is morally infallible and that liberals are, by definition, pitted against sinister and — more importantly — powerful forces, then it’s easy to explain away what seem like double standards. Any lapse, error, or transgression by conservatives is evidence of their real nature, while similar lapses, errors, and transgressions by liberals are trivial when balanced against the fact that their hearts are in the right place.

Despite controlling the commanding heights of the culture — journalism, Hollywood, the arts, academia, and vast swaths of the corporate America they denounce — liberals have convinced themselves they are pitted against deeply entrenched powerful forces and that being a liberal is somehow brave. Obama, the twice-elected president of the United States, to this day speaks as if he’s some kind of underdog.

A later column titled Blaming America First  had these additional points  :

In reality, the liberal ideological comfort zone is incredibly narrow. If an issue can’t be turned into a critique of America (or: white privilege, the religious Right (variously defined), capitalism, the GOP, or some other float in the parade of horribles that is the legacy of those horrible Pale Penis People who gave us so much of Western civilization), then the conversation must be pulled in that direction. It’s simply where their minds go. Rhetorically they have to fight every fight on home turf.
...
 So what happens when events and facts make it impossible for liberals to change the subject to more convenient topics? They figure out how to make the villain or problem at hand “conservative.”
...
 All of the nonsense about microaggressions and hate speech, all of the namby-pamby self-esteem boosting, the elevation of feelings, the paranoia of offending people, the thousand flavors of political correctness including informed-consent for every romantic overture: They did it. Them. All by themselves. And they are still doing it. Conservatives aren’t behind any of it and libertarians certainly aren’t.

But the moment it becomes impossible to ignore the huge frick’n mess they created, what do they start calling it? Conservatism.

This is all part of the narrative and political branding.  Plenty of bright people are so trapped in the bubble that they can't see this at all.

Later in the same column he continues:

The Left loves wars of national liberation. The Left loves self-determination against colonialism. But when such nationalism becomes a problem, out come the smug lectures about how nationalism is right-wing.

 And that’s the point. Once something becomes too terrible to ignore, it must be labeled “right-wing” or “conservative” somehow. If you don’t believe me, find the smartest liberal you know and ask him or her to list all of the really bad things done by the Left. Odds are you’ll get silence. Or you might get “Well, I don’t believe in labels . . . ” (“Don’t get him started on that again, people!” — The Couch). But what you won’t hear is much of anything about the American eugenics movement, or the internment of the Japanese, or the Black Panthers, Weathermen, the manifest failures of the New Deal (economic and non-economic alike), etc. That’s because liberalism, by conviction if not definition, is never wrong.

Kevin Williamson in a column titled The New Royals :

Other civilizations are big on karma, arete, martial codes of honor, virtus, etc.; we Americans have “Work hard, live well, enjoy good stuff,” which might be sneered at by philosophers and warlords but is nonetheless the best and most humane organizing principle a human polity has yet discovered.

I miss the days when the important status symbol could be something so simple as a Cadillac.
...

Tinkering with the organic, spontaneous orders of human society is a tricky business. In the 1960s, the Western world got it into its collective head that traditional social arrangements, especially family arrangements, were an instrument of oppression that needed to be torn down. And we set about tearing them down, without giving any thought to what would replace them. We were confident that whatever came next inevitably would be better, and about 80 percent of our current domestic-policy initiatives are in one way or another aimed at dealing with the fact that what came after wasn’t better — that it was brutish and frequently cruel — without ever being so gauche as to notice that that’s the case.

Similarly, the old status symbols — the nice house, the car, the sensible two-week family vacation — might have been bound up with a brand of unthinking and insalubrious materialism, but they were also bound up with some important virtues that we are in the process of rediscovering: thrift, frugality, delayed gratification, etc. That is, in fact, why status symbols work as status symbols: It’s not just having the Cadillac or the gold watch — it’s being the sort of person who earns them.
...
 As in the case of the princess in Hans Christian Andersen’s 1835 story, so sensitive that she could feel the pea under 20 mattresses and 20 featherbeds, acute dissatisfaction with the tiniest, most ridiculous little details of life is how 21st-century progressives communicate to the world that they are indeed the new royalty, with sensibilities finer than those known to mere commoners.
...
 There is a term for this that is uncharitable but cannot be improved upon: status-whoring. The old status symbols may have been shallow; the new ones are shallow, destructive, and a great deal less fun to drive.

And they don’t even require you to work particularly hard in school.
...
 But there is an important distinction between political-correctness-as-status-symbol and Cadillac as a status symbol. The Cadillac, at least as presented by Neal McDonough, is a symbol of what you have earned; hashtag-activist foie-gras phobia is, like the princess’s sleepless night, an expression of who you are — or who you are pretending to be. Anybody can be dissatisfied; it requires no real expenditure of effort. All you have to do to be a member of the new aristocracy is to convince the prince (or some gender-neutral equivalent) that you belong.

Which is to say, our progressives have progressed right back to 1835.

 These examples are presented in support of what the late Andrew Breitbart described as the frequent practice of the left to exhibit an "unearned moral and intellectual superiority."  This kind of posturing is an attempt to always claim the high ground in all matters.  It's as phoney as heck and it's all pretend even if many of practitioners don't realize this.

This Afterburner video with Bill Whittle explains this Coin of the Realm.


Once matters get beyond modest complexity, there are no shortcuts to acquiring the requisite knowledge and achieving sufficient maturity and wisdom to make sound judgements about right and wrong and to then have sound ideas about what might follow.  That is what I told my youngest child, who is a junior in college.  All that has comprised this post was part of an attempt to give him an explanation of and a vocabulary to describe and deal with an attitude he senses on campus which he calls "The Smug." 

Cost of this effort: some time; look on his face afterwards: priceless!

Chart of the Day

(HT: Cafe Hayek)

I'm not sure what the caption should be though. I was thinking one of the following:

More people, more wealth

Exploding towards Malthusian disaster

The rich get richer and the poor get richer

The rich get richer and the poor get relatively poorer

Yet another chart whose meaning is in the eye of the beholder

Or something else. What do you think?

Great Guys Announce a Major Staff Realignment

As a result of output both shabby and sporadic, from a place people care so little about that it isn't even in the right place on most maps, the Great Guys Board of Directors announces with some relief that Hey Skipper will in the near future be spending more time with his family.

In Germany.

Where he will continue his output both shabby and sporadic.

War of the Sexes: Part 8 - In Defense of Non-Monogamy

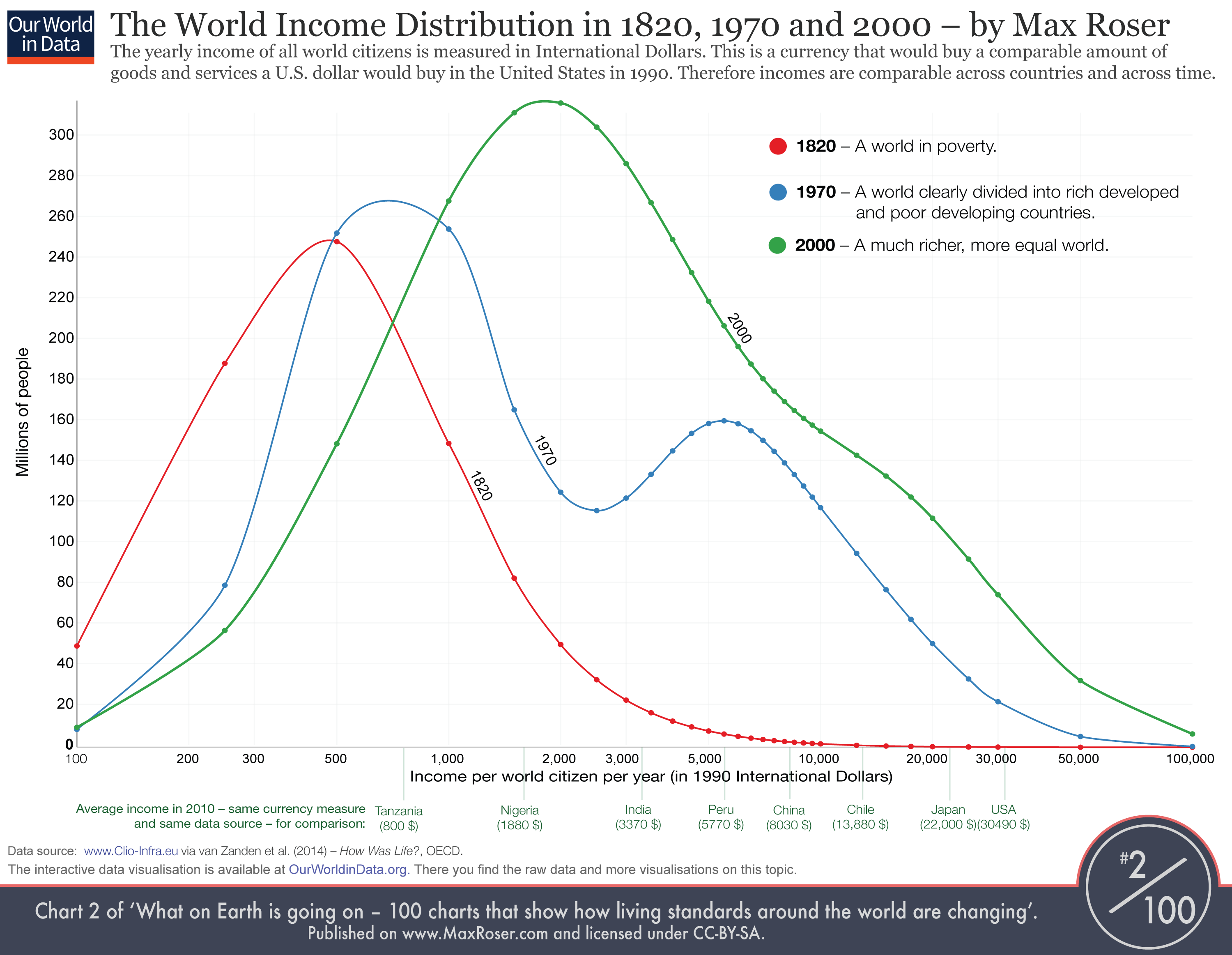
There are several things to consider when humans choose their own monogamous partners. One of those is assortative mating:

Assortative mating is a nonrandom mating pattern in which individuals with similar genotypes and/or phenotypes mate with one another more frequently than would be expected under a random mating pattern.

Assortative mating almost certainly happens:

The old saw notwithstanding, opposites do not really attract when it comes to love and marriage. Likes attract. In one of the classic papers, originally published in 1943, two sociologists studied 1,000 engaged couples in Chicago, expecting to find at least some traits in which opposites did indeed attract. But out of fifty-one social characteristics studied, the sign of the correlation was positive for every single one. For all but six of the fifty-one traits, the correlations were statistically significant. [...] 

Of the many correlations involving husbands and wives, one of the highest is for IQ. [...]

Christine Schwartz and Robert Mare examined trends in "assortative marriage," ... from 1940 to 2003. They found that homogamy has increased at both ends of the educational scale -- college graduates grew more likely to marry college graduates and high school dropouts grew more likely to marry other high school dropouts. [...]

In 1960, just 3 percent of American couples both had a college degree. By 2010, that proportion stood at 25 percent. The change was so large that it was a major contributor to the creation of a new class all by itself. [...] 

Bit increased educational homogamy ... inevitably means increased cognitive homogamy.

I'd like to go beyond just considering cognition though. Imagine all successful people across all human endeavors. Leave out those that are successful overwhelmingly due to luck. Consider all positive traits that are more common among those successful people than the general population. Those traits no doubt have at least some intersection with cognition and the "fifty-one social characteristics" above and might include things like perseverance, impulse control, drive, learning ability, creativity, curiosity, ability to work in teams, leadership, followership, etc.

Let's call that suffectiveness. Suffectiveness is a combination of "success" and "effectiveness" or those human traits that are generally effective towards achieving success given the current state of civilization. It ignores specific characteristics that are useful in specialized endeavors. Ability to play brass instruments would be an example of a characteristic which is good but not part of suffectiveness.

If mating were completely random, the distribution of suffectiveness would likely resemble a bell curve. If suffectiveness is at least partly heritable and if assortative mating occurs to some extent (which it does), the distribution of suffectiveness would change.

Is suffectiveness heritable? To some extent, very likely. For example, IQ is likely at least partly related to one of the sub-traits of suffectiveness and IQ is very likely at least partly heritable:

The general figure for heritability of IQ is about 0.5 across multiple studies in varying populations.

I decided to do some modeling. There's no way to completely accurately model the suffectiveness of a human population, so I made some simplifying and extreme assumptions.  The model population is 100,000 for each generation, with each female having exactly two children. Each individual has 23 pairs of chromosomes, coincidentally the same number of chromosomes that humans have. On each chromosome, there are arbitrarily 12 gene complexes that add to the suffectiveness of the individual if present. The total suffectiveness of the individual's genotype is the sum of all present suffective gene complexes across all of the chromosomes.  I'm not considering dominant and recessive genes for this model. Since there are 46 chromosomes (23 pairs), and 12 gene complexes per chromosome, there can be a maximum of 552 suffective gene complexes present.

Each individual is able to exactly tell the suffectiveness of another individual just by observation, except that a small random amount of suffectiveness is added to the sum of the suffective gene complexes. The small random amount for these trials had a mean of zero and a variance of 2.76 gene complexes. This was added mostly to keep the curves smooth but the original reason was to keep the sorting from be too rigid and to provide a distinction between genotype and phenotype. I call the total suffectiveness including the random addition the phenotype suffectiveness.

The first model is an assortative monogamous mating model. Each generation is sorted by phenotype suffectivness. One of each of the 23 alleles is taken whole (no chromosomal crossover) from each paired male and female when generating the chromosomes for the offspring. The following graphs show the phenotype suffectiveness for generations 1 (the original), 2, 3, 9, 33, 129, and 257.

Assortative Mating - Original Distribution

Assortative Mating - Generation 2 Distribution

Assortative Mating - Generation 3 Distribution

Assortative Mating - Generation 9 Distribution

Assortative Mating - Generation 33 Distribution

Assortative Mating - Generation 129 Distribution

Assortative Mating - Generation 259 Distribution

The variance of suffectiveness increases each generation, though it changes little after about the 100th generation as this seems to be the point where the distribution of chromosomes can't be improved upon without chromosomal crossover.

In the model above, no chromosomal crossover was allowed. In other words, alleles were never allowed to be formed by mixing any of the gene complexes. In real life, some crossover does take place. In the second model, I allowed an extreme version of chromosomal crossover, where any of the suffective gene complexes were randomly allowed to crossover intact.

The results did not differ noticeably for about 30 generations, where the changes in distribution from selection of entire chromosomes was such a large factor that crossover had relatively little effect. After the 30th generation or so, the differences relative to the first model became more apparent. The following graphs show the suffectiveness for generations 33, 129, and 257, 513, and 1025.

Assortative Mating with Crossover - Generation 33 Distribution

Assortative Mating with Crossover - Generation 129 Distribution

Assortative Mating with Crossover - Generation 257 Distribution

Assortative Mating with Crossover - Generation 513 Distribution

Assortative Mating with Crossover - Generation 1025 Distribution

Chromosomal crossover enables further concentration of the suffective gene complexes (and lack thereof) leading to an even wider variance and more extreme distribution of suffectiveness. Perhaps in enough generations, these two extremes will resemble H.G. Wells' Morlocks and Eloi?

The two models above were monogamous mating models. Even without the genetic drift shown by the models, assortative monogamy still leads to inequality. Even with wealth redistribution, there will still be a radical inequality of suffectiveness per household. At one end, Ph.D.'s marry Ph.D.'s, at the other end, unemployed sewer workers marry part-time barmaids. Not that there's anything wrong with sewer workers and barmaids, but the point is that the two households will have nothing in common and will hardly even be able to talk to each other. It will likely only get worse over time even with no genetic component. I believe that this sort of inequality will be both an inherent feature of monogamy going forward and that this inequality is far more destabilizing than mere wealth inequality.

Many societies in the past and present are not monogamous and as I've pointed out in other posts, monogamy is becoming less popular now in the United States (and the rest of the world) as well. Monogamy has many good points and was, in my opinion, very likely necessary for civilization to have made it this far. But here we are, and it's not clear to me that it makes sense going forward because it will inherently lead to a particularly destabilizing sort of inequality.

Lets' go back to models. This next model models female hypergamy, which, for the purposes of this post is defined as the natural desire for females to mate with someone of higher status, perhaps or hopefully much higher status. It's debatable to what extent that desire is present in human females, but that's the assumption for the next model.

This model is just like the first model except that only the top fifth of suffective males are used to generate the next generation of offspring. In the first model, each male and female had two children. In this model, each female still has two children. However, each of the top 20% most suffective males has ten children, two with each of five females.

In the graphs from the previous two models, the axes were identical. For this model, the Y-axis expands as the distribution narrows. The following graphs show the suffectiveness for generations 1, 2, 3, 9, 33, and 129 from the female hypergamy model.

Hypergamy - Generation 1 (Original)  Distribution

Hypergamy - Generation 2 Distribution

Note that by the 2nd generation (1st iteration), there is already a significant shift of suffectiveness in the positive direction.

Hypergamy - Generation 3 Distribution

Hypergamy - Generation 9 Distribution

Hypergamy - Generation 33 Distribution

Hypergamy - Generation 129 Distribution

The genetic distribution of suffectiveness moves rapidly in the positive direction every generation until it maxes out what the genome can support without mutations (after about the hundredth generation, there's not much change). Note that these results are without chromosomal crossover. With crossover, the results are pretty much the same, they just happen faster and are even more extreme.

As I mentioned before presenting these models, there are many simplifying and extreme assumptions incorporated into the models. The point is not that the above is a reflection of reality, or to the extent it is a reflection, it's a very, very distorted one. The point of modeling is to get an idea of how potential factors might affect the trajectory of society.

Each person interprets the ideas and information available differently. My interpretation is that monogamy will probably lead to a more unequal society over time and that the particular type of inequality (inequality of suffectiveness and status) will be destabilizing and may more than cancel out the advantages of monogamy, and that women seeking out much higher status males to get them pregnant may not be such a bad thing if we can survive a few generations of that, especially if the other 80% of men are happy to go their own way each generation and play video games and watch porn.

War of the Sexes: Part 7 - Civilization

One of the problems of anthropology and other sciences that look back in time is that there are a lot of "just-so" stories. Especially in anthropology, there are such huge holes in the data that lots of narratives can be created to fit the evidence. As a result, many of those narratives are little more than educated or sometimes wild-ass guesses. On the bright side, while not at all an expert in anthropology, I do consider myself an expert in wild-ass guessing, so I fit well in that field. I cheerfully admit that the rest of this post is nothing more than guessing by me and various experts in the field.

The first humans and proto-humans were monogamous hunter-gatherers. The just-so story goes that since they were often hunting animals much larger and faster than they were, they needed the whole tribe to rally, especially the males, in order to bring the mammoth (literally) beasts down. They also needed to defend the tribe against predators. To keep all of the males maximally engaged in a tight and large tribe, the males and females paired off in monogamous relationships, and they lived happily ever after. In the 20th century, 10 different remote hunter-gathering tribes were discovered, and they were indeed mostly monogamous.

Then herding and agricultural were invented and it all went to hell for a number of reasons. The male teamwork required for hunting was no longer needed for survival. Women were able to do farm work and were more than self-sufficient so they didn't need men to hunt for them.  In addition, people started having possessions and wealth disparities were introduced, so that a "rich" or alpha male could afford and/or entice multiple women.  So monogamy went out the window and was replaced by polygamy in primitive herding and agricultural societies. Once again, a number of remote tribes of these varieties were discovered in the 20th century and were mostly polygamous.

Unfortunately, the polygamous cultures didn't live happily ever after. Humans, regardless of mating patterns, go to war over resources. One of the problems of polygamy is that one resource is always in short supply: women. If the men at the top have multiple women, the men at the bottom have zero women, and even the men at the top would prefer more women, always more, more, more. As a result, these tribes are often in a state of continuous warfare: they are at war every day and have been at war as long as anyone can remember. The most famous of these tribes is the Yanomamo discovered in the mid-1960s by Napolean Chagnon:

According to Chagnon, when he arrived he realised that the theories he had been taught during his training had shortcomings, because contrary to what they predicted, raiding and fighting, often over women, was endemic. ... As Chagnon described it, Yanomamö society produced fierceness, because that behavior furthered male reproductive success. According to Chagnon, the success of men in violent interaction and even killing, was directly related to how many wives and children they had. At the level of the villages, the war-like populations expanded at the expense of their neighbors. Chagnon's positing of a link between reproductive success and violence cast doubt on the sociocultural perspective that cultures are constructed from human experience. An enduring controversy over Chagnons' work has been described as a microcosm of the conflict between biological and sociocultural anthropology.

There are a number of possible problems with large groups of men with no access to women. At best, they just sulk off on their own but have no interest in supporting or defending society. At worst, they turn on society and damage or destroy it. In the right hands, they can be used as a resource to attack other tribes, to loot and plunder, or possibly to jihad against infidels. All of these have happened many times throughout history with polygamous societies.

You may have noticed that advanced, stable, prosperous societies from the far east to the far west are usually mostly monogamous (at the very tippy top of the ruling class, there're often mistresses, concubines, slaves, etc. but it's monogamy for the vast majority of the people). Somehow, we got from pathological polygamous societies back to monogamy. Anthropologists have lots of just-so stories about how that happened, but given the success of monogamist societies relative to non-monogamous ones, it seems that getting from primitive agriculture to the industrial age was not hindered and possibly aided a lot by the stability provided by monogamy.

But now we're transitioning from the industrial age to the information age and I wonder if there are some parallels to the transition from hunter-gathering to primitive agriculture. The engagement of males was required for hunting for hunter-gatherers and industrial age males were likely required for a lot of the heavy lifting required for factories and the more advanced high-production agriculture required to support all those workers in the factories. On the other hand, full engagement of males was not required for primitive agriculture and now is not required for the vast majority of jobs in the information age. The transition from hunter-gathering to primitive agriculture was accompanied by a transition from monogamy to non-monogamy. Is there any reason we should be surprised by a similar transition from monogamy to non-monogamy going forward?

It's already happening at a rapid rate. For example, 72.3 percent of non-Hispanic blacks are now born out-of-wedlock, with the black mother often having multiple children, each with a different alpha (to her) father. It's pretty much a perfect example of a non-monogamous mating system. Other ethnicities are behind in the polygamous revolution under way, but they are catching up.

Fortunately, with the availability of ever more immersive entertainment, most of the displaced males (Men Going Their Own Way), will hopefully just sulk off and not cause any major damage.

Too Busy to Loot, Rape & Pillage

Unfortunately, they may not be much interested in supporting the culture that's pushing them away. For example, they may work a lot less, making just enough to support themselves, which could reduce the tax base. That may be a problem: one reason that the 72.3% of blacks born out-of-wedlock is not a catastrophe is that the mothers and children are able to get support from the safety net if needed. If there's not a large enough tax base, that safety net may be difficult to maintain.

Competition and attack from other societies may also be a problem. A culture where a large number of males are disengaged is not going to be competitive with a culture that keeps the males involved. Will men rise to defend America if they've gone their own way? Will women be able to defend America if the men won't?

I suspect civilization will survive just fine in some form or other but time will tell.

War of the Sexes: Part 6 - Male Entertainment

In the article "Shock study: Marriage rate declines with porn use, threatening economy, society," we learn that:

Pornography is replacing the desire among young men for marriage, according to a new study that finds males are chasing “low-cost sexual gratification” on the web over a wife and family.

There we have our answer.  Men are going their own way because of porn. Case closed!

Or maybe not. While the authors make a herculean effort to show causality, a closer look at the actual study finds the following in the conclusion regarding porn causing a decline in marriage rates:

... the causality likely runs in the direction that we assert. We stop short of saying that we have accurately identified the magnitude of the causal effect.

In other words, they're only guessing which way causality, if any, runs. So never mind. We still don't know if porn lowers marriage rates, lower marriage rates cause increased porn usage, or they're just coincidentally correlated.

Indeed, from table 4 in the study, it seems that any Internet usage (for example, viewing financial sites) by men correlates with lower marriage rates except for viewing religious sites (there's that religion thing again). I'd also be willing to bet that increased use of sports facilities, watching sports TV and TV in general, watching movies and other entertainment, playing electronic games, and probably even working crossword puzzles all correlate with reduced rates of marriage.  In other words, if men aren't married, they're going to fill their extra time with something.  And perhaps, just perhaps, if they spend their time doing stuff they find enjoyable, they won't bother getting into the dating game and marriage. What a surprise! Shocking even, eh?

So clearly, we should ban not only porn, but also sports, TV, movies, games, etc. for men. Indeed, we should ban all activities that males might possibly find enjoyable so that they can focus on women. I'm sure that'll eliminate the "shocking" threat to society of falling marriage rates. Unless, in their spare time, the very bored and frustrated males instead decide to destroy civilization, pillage and rape (increased use of porn correlates with lower rates of rape, for example).

If it is true that porn (and games, movies, etc.) reduce marriage rates, then it will probably only quickly get worse. Movies, games, and porn are rapidly co-evolving with each other and virtual reality to become ever more realistic and immersive. Female (and male) actors won't even be needed for porn or probably even movies in general in the not too distant future. Porn games will probably be created to be customizable active porn movies with perfect 10 virtual stars whose actions will be directed by the gamer. Once there are no humans involved in the entertainment, it will be really hard, if not impossible, to regulate and/or ban.

Men who go their own way will have an ever more realistic virtual reality to retreat into and perhaps they will indeed by happier there.

War of the Sexes: Part 5 - Young Female Fantasy Fiction

Let me tell you a story.

Once upon a time, there was a young woman who got into a spot of trouble. She was rescued by a prince and they got married and lived happily ever after. The End.

Oh. You've heard the story before? Yeah, never mind the lack of detail, I might be a few dozen millennia late for that to be an original story.  Indeed, that story and a few variations (knight in shining armor instead of prince, for example) have been told over and over again, I think probably since shortly after language evolved enough complexity to tell it.

I have a number of alternate plots.  She could've been saved by the big-hearted pauper and then gone on to starve on the streets.  She could've been saved by the kindly serf farmer and then died from infection after giving birth to her second child.  She could've been saved by a courageous merchant who then fell afoul of the king and was beheaded forcing her into a life of prostitution to stay alive.  All of these would be much more realistic (and in my opinion better) stories, but no, the big favorite is that she's saved by, and then marries, wealth and power, and then lives happily ever after. Yeah, right, like that ever actually happened. Nonetheless, that's the favorite fantasy of the ages.

True love's first kiss usually makes a showing as well. How can anyone feel true love at their first meeting? Well, the prince is such a better catch than anyone else in the kingdom that I'm sure the young woman did indeed feel true love.  For the prince, it was probably true lust.  Close enough for government work.

In the modern age of feminism, you would think stories like that would be banned or at least rewritten.  They are, to some extent.  For example, Disney's Tangled is a rewritten version of Rapunzel to have the savior be a reforming thief, rather than a prince.  However, books are one area where feminism has had minimal impact.

One of the genres I like to read for fun is Science Fiction/Fantasy leaning towards Fantasy.  Think Harry Potter. Or maybe King Arthur and Merlin.  The Fantasy end of the genre is overwhelmingly populated with the story I told above.  Except it wasn't necessarily "once upon a time" (it's often set in modern times) and instead of a prince, it's a superhuman alpha-male.  Or two.  Or more. All fighting over the girl.

Unlike the young women in stories of old, the young women in these stories have few, if any redeeming qualities.  They're usually whiny, bitchy, weak, incompetent, untalented, and the plot generally is built around her continually doing really foolish and stupid things that puts her in mortal danger requiring repeated rescues by the alpha-male(s) at great cost to them.  She sometimes has agonizing difficulty deciding whether or not to be in a "relationship" with the alpha-male hero, and if there's more than one interested in her, it's a heroic struggle on her part deciding which, if either, to commit to.

The alpha-males are not only the strongest superheros ever imagined, they're also intensely loving (they'd give their lives for her), tender, emotionally intimate, incredibly devoted, impossibly patient (they'll wait for her forever if they have to and if she chooses the other alpha, that's okay - they'll still be there for her), and of course handsome, talented, etc.  Even though she has no or few redeeming qualities, they love her because, well, um, just because.  Maybe just because she exists.

One of the most popular fantasy romance is the Twilight series by Stephenie Meyer and closely follows the above description.  But it is neither the first nor the last of its kind.  In the sub-sub-genre of paranormal romance, Amazon lists 95,338 titles, most from "indie" authors, and from what I can tell, most of those were written since 2010. From what I can unfortunately tell, over 80% of those follow the above description pretty closely.  I use the term "unfortunate" because so many of the books have descriptions that sound pretty good, so I read (at least part of) them, before becoming frustrated with reading about yet another completely lame young woman.  At this point, if it's a female author and a female protagonist anywhere in the realm of Science Fiction/Fantasy, I won't read the book. Ever.

95,338. That's just paranormal romance and doesn't include other teenage girl romance titles. Hundreds of these books are released every day and hundreds of thousands or even millions (on the days surrounding a popular release) of young women finish reading one of these books every day. Why would any self-respecting female author write something with such a weak and incompetent young woman?  Because it sells, that's why.

This post is an interlude in this series, just a tidbit.  It may be a puzzle piece in the War of the Sexes, it may not be.  If it is a puzzle piece, I don't really know how it fits.  Perhaps it's a primary persistent fantasy of a substantial percentage of teenage girls since the beginning of time/language, which might indicate that the feminist narrative will always find some competition in the female psyche of a substantial part of the population (after all, it's always members of the patriarchy that comes to the rescue). Perhaps teenage girls going their own way (from men) have nothing else to do and are retreating into this fantasy reading.  Perhaps teenage girls are influenced by these books and end up with unreasonable expectations about men fueling the War of the Sexes.

Or perhaps it's just entertainment, though at best, certainly not entertainment of which feminists would approve.

Common Genius: episode ##,###,###

A recent column by Bret Stephens about yet another example of American resilience contained the following:

Imagine an economic historian in the year 2050 talking to her students about the most consequential innovations of the early 21st century—the Model Ts and Wright flyers and Penicillins of our time. What would make her list?

Surely fracking—shorthand for the combination of horizontal drilling and hydraulic fracturing that is making the U.S. the world’s leading oil and gas producer—would be noted.
...

 Fracking would make a good case study. The revolution happened in the U.S. not because of any great advantage in geology—China, Argentina and Algeria each has larger recoverable shale gas reserves. It didn’t happen because America’s big energy companies are uniquely skilled or smart or deep-pocketed: Take a look at ExxonMobil ’s 2004 Annual Report and you’ll barely find a mention of “fracturing” or “horizontal” drilling.

Nor, finally, did it happen because enlightened mandarins in the federal bureaucracy and national labs were peering around the corners of the future. For the most part, they were obsessing about the possibilities of cellulosic ethanol and other technological nonstarters.

Instead, fracking happened in the U.S. because Americans, almost uniquely in the world, have property rights to the minerals under their yards. And because the federal government wasn’t really paying attention. And because federalism allows states to do their own thing. And because against-the-grain entrepreneurs like George Mitchell and Harold Hamm couldn’t be made to bow to the consensus of experts. And because our deep capital markets were willing to bet against those experts.
...

Here, then, is the larger lesson our future historian will draw for her students: Innovation depends less on developing specific ideas than it does on creating broad spaces. Autocracies can always cultivate their chess champions, piano prodigies and nuclear engineers; they can always mobilize their top 1% to accomplish some task. The autocrats’ quandary is what to do with the remaining 99%. They have no real answer, other than to administer, dictate and repress.

A free society that is willing to place millions of small bets on persons unknown and things unseen doesn’t have this problem. Flexibility, not hardness, is its true test of strength. Success is a result of experiment not design. Failure is tolerable to the extent that adaptation is possible.

This is the American secret, which we often forget because we can’t imagine it any other way. It’s why we are slightly shocked to find ourselves coming out ahead—even, or especially, when our presidents are feckless and our policies foolish.

We are larger than our leaders. We are better than our politics. We are wiser than our culture. We are smarter than our ideas.

This is yet another example of the Common Genius described by Bill Greene and referenced in an earlier post.  Having read the book back then and recently reread parts, I would say that on balance the author did a fine job making his point.  Reiterating that point with some limited excerpts:

A major theme of these pages is that all historical progress has bubbled up from the bottom—from the actions of common men and women. A secondary theme is that most of history's evils have flowed from the top—from the intelligentsia, organized groups, and soft-science experts who arise in mature societies and are the pied pipers of their decline. In the final chapters, we will examine how the decline of free societies has often resulted from the transfer of authority and leadership from those who built the society to a destructive intelligentsia who arrive after the heavy lifting is done. The arrival of the intellectuals also marks the time when knowledge and decision-making appears to enter a steep decline. The notion that intellectuals are wise and should be listened to is a persistent, recurring, and insidious error that has doomed most past civilizations.

I do not mean to demean all people of intellect—most of them are great assets to their communities. However, there is reason to beware those with little practical experience in any field, who parade their "expertise" before the public, and operate primarily as critics rather than participants.

...
 
Throughout history, such leaders have made life as difficult as possible for the bulk of humanity. The expression of man's genius had to be fought for, and opportunities for its release have been restricted to a few brief moments and places in time. Such moments were the "accidents" of history, but there was nothing accidental about what subsequently happened. The achievements were never pre-ordained but arose from a long-term struggle by ordinary people to advance, one step at a time, over thousands of years. But wherever individual men and women got even a little such opportunity, freedom and prosperity followed. They built it piece by piece, not by trying to apply utopian theories, but by solving one problem at a time and moving ever forward.
Now, this is a revolutionary idea and perhaps in a perverse way, will delight most of the average Joes out there who are pestered by those "beautiful people" who want to tell them what to do and how to do it.

Dinocrat concluded a recent post with the following observation:

The US soi-disant intelligentsia and the US average Joes are probably more likely split against each other on some critical issues (95-5 one way, 62-38 the other) — are you de Blasio or a cop, for example. Perhaps the danger Diamond senses but (can)not articulate is in the self-styled intellectual elites losing big for a long time if the average Joes found a guy with a clear mind and strong voice. Pity Walter Williams is probably a little too old to run.

This hints at a future pregnant with the possibility of unleashing much more common genius.  You know - if we had a revolt of the masses against the elites, middle class American style!

(A "revolt against" being a part of this previous post)